Formuły w programie Dietrich’s są świetnym miejscem do centralnego zarządzania wartościami wprowadzanymi do modelu. Mogą wykorzystywać zmienne systemowe oraz zmienne tworzone przez użytkowników. Wszędzie tam, gdzie przy polu wprowadzania wartości pojawia się ikonka kalkulatora możemy użyć formuły.
Pozwalają one jednak na znacznie więcej. Można w nich zawierać warunki, których spełnienie lub nie, da precyzyjnie zaplanowaną wartość.
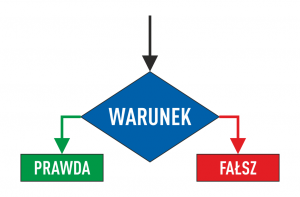
Warunki w formułach
zapis formuły warunkowej sprowadza się do utworzenia trzech następujących po sobie nawiasów okrągłych () oddzielonych średnikami ;
(warunek);(prawda);(fałsz)
- pierwszy nawias to formuła warunkowa/porównawcza badająca zależności miedzy wybranymi przez użytkownika wartościami
- drugi nawias to wartość, którą zwróci cała formuła gdy warunki z pierwszego nawiasu zostaną spełnione
- trzeci nawias to wartość, którą zwróci cała formuła gdy warunki z pierwszego nawiasu nie zostaną spełnione
warunek można komplikować zagnieżdżając w jego strukturze kolejne warunki. Dzięki temu można uwzględnić wiele okoliczności.
Przykłady: ((warunek1)&(warunek2));(prawda);(fałsz) (warunek1);((warunek2);(prawda1);(fałsz1));(fałsz2) (warunek1);(prawda1);((warunek2);(prawda2);(fałsz2)) (warunek1);(prawda1);((warunek2);(prawda2);((warunek3);(prawda3);(fałsz3)))
Operatory porównawcze
| symbol | znaczenie | opis |
| = | równe | warunek jest spełniony jeśli obie strony równania są takie same |
| != | różne | warunek jest spełniony jeśli obie strony równania są różne od siebie |
| > | większe niż | warunek jest spełniony jeśli lewa strona jest większa od prawej |
| >= | większe niż lub równe | warunek jest spełniony jeśli lewa strona jest większa lub równa prawej |
| < | mniejsze niż | warunek jest spełniony jeśli lewa strona jest mniejsza od prawej |
| <= | mniejsze niż lub równe | warunek jest spełniony jeśli lewa strona jest mniejsza lub równa prawej |
Przykład: zmienna V_a ma wartość 0.04[m] (V_a>=0,02[m]);(20[cm]);(0[cm]) -> 20[cm] (V_a!=0,04[m]);(20[cm]);(0[cm]) -> 0[cm]
Operatory matematyczne
| symbol | znaczenie | opis |
| + – * / | dodawanie, odejmowanie, mnożenie, dzielenie | podstawowe działania matematyczne |
| ( ) | nawias okrągły | grupuje działania matematyczne, określa kolejność, zagnieżdża części składowe formuły |
| [ ] | nawias kwadratowy | określa jednostkę wartości liczbowej np: 0.1[m] lub 0.1[cm] |
| sin, cos, tan | Sinus, Cosinus, Tangens | funkcje trygonometryczne – wartość kata podawana jest w stopniach (koło = 360°) |
| asin, acos, atan | Arcus Sinus, Arcus Cosinus, Arcus Tangens | funkcje cyklometryczne – wartość kata podawana jest w stopniach (koło = 360°) |
| sqrt | pierwiastek kwadratowy | sqrt(25) daje wartość 5 (√25 = 5) |
| ^ | potęga | 5^2 daje wartość 25 |
| Pi | stała Pi | Pi = 3.1415 – np.: obwód koła o średnicy 2.5m obliczane jest jako Pi*2.5[m] |
| round | zaokrąglenie |
poziom istotności zaokrąglenia jest stały i wynosi 0 – liczba jest zaokrąglana do jedności np.: round(2.4) daje wartość 2; round(2.5) daje wartość 3; round(2.4+0.5) daje wartość 3 |
| abs | wartość bezwzględna | wartość bez znaku (bez minusa) abs(25) daje wartość 25 abs(-25) daje również wartość 25 |
Przykład: zmienna V_a ma wartość 0.04[m] (V_a*2<0.08[m]);(20[cm]);(0[cm]) -> 0[cm]
Operatory zapytań tekstowych
| symbol | znaczenie | opis |
| ~ | lista | pozwala na tworzenie listy wyszukiwanych wartości; odnalezienie choćby jednej wartości powoduje spełnienie warunku np.: abc~bca~cab |
| * |
symbol zastępczy /wieloznacznik |
skraca szukaną wartość do kilku konkretnych znaków, znaki nieistotne można pominąć w ten sposób: a*=abc *c=abc *b*=abc |
| { } | nawias klamrowy |
pozwala tworzyć złożone wyszukiwania w warunku np.: warunek1=(V_tekst={abc~bca~cab}) warunek2=(V_tekst={*b*}) |
| “ „ | cudzysłów | liczba zapisana w cudzysłowie jest traktowana jako tekst; pozwala zapisać warunek, w którym znakami do wyszukania są tylko liczby (jeśli zapytanie składa się z cyfr oraz innych znaków nie trzeba ich zapisywać w “ „) |
Przykład:
zmienna V_tekst ma wartość abc
(V_tekst={abc~bca~cab});(20[cm]);(0[cm]) -> 20[cm]
(V_tekst={ab*});(20[cm]);(0[cm]) -> 20[cm]
(V_tekst="1.23");(20[cm]);(0[cm]) -> 0[cm]
wskazówka: Teksty są sortowane alfabetycznie, dzięki czemu można je również porównywać pod kątem „większy” i „mniejszy”. Tekst, który jest pierwszy w kolejności alfabetycznej, jest mniejszy. Np.: „abc” jest „mniejsze” niż „bca”
Przykład: zmienna V_tekst ma wartość abc (V_tekst<bca);(20[cm]);(0[cm]) -> 20[cm] (V_tekst>bca);(20[cm]);(0[cm]) -> 0[cm]
Operatory logiczne
| symbol | znaczenie | opis |
| & | logiczne „i“ | oznacza wymóg spełnienia wszystkich warunków rozdzielonych tym znakiem |
| | | logiczne „lub“ | oznacza wymóg spełnienia choćby jednego z warunków, z wszystkich rozdzielonych tym znakiem |
Przykład:
zmienna V_tekst1 ma wartość abc
zmienna V_tekst2 ma wartość cab
((V_tekst1={a*})|(V_tekst2={b*}));(20[cm]);(0[cm]) -> 20[cm]
((V_tekst1={a*})&(V_tekst2={b*}));(20[cm]);(0[cm]) -> 0[cm]
((V_tekst1={a*})&((V_tekst2={b*})|(V_tekst2={c*})));(20[cm]);(0[cm]) -> 20[cm]