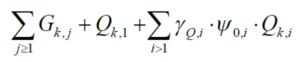Obliczenia konstrukcji budowlanych należy wykonać z uwzględnieniem różnych wariantów obciążenia zwanych kombinacjami obciążeń. Algorytm budowania kombinacji obciążeń dostosowany jest stanu granicznego podlegającego analizie: SGN oraz SGU. Szczegółowe wytyczne w tym zakresie zawiera norma PN-EN 1990, Podstawy projektowania konstrukcji. DC-Statik usprawnia proces projektowania konstrukcji budowlanych poprzez automatyczne zebranie obciążeń oraz gotowej kombinatoryce obciążeń jaką posiada.
Stan graniczny nośności (SGN) – kombinacje obciążeń
Kombinacje obciążeń dla stanu granicznego nośności uwzględniają obliczeniowe wartości obciążeń stałych oraz zmiennych. Prawdopodobieństwo pojawienia się obciążeń zmiennych określone jest współczynnikiem jednoczesności obciążeń.
oznaczenia:
γGj , γQi– współczynnik bezpieczeństwa
Gkj – obciążenia stałe
Qkj – obciążenia zmienne
Ψ0i – współczynnik jednoczesności obciążeń
Przykładowa kombinacja obciążeń dla schematu obliczeniowego – KROKIEW
| Nr kombinacji | Formuła kombinacji |
|---|---|
| 1 | 1.35 g |
| 2 | 1.35 g + 1.50 sv |
| 3 | 1.35 g + 1.50 s1 |
| 4 | 1.35 g + 1.50 s2 |
| 5 | 1.35 g + 1.50 w000d |
| 6 | 1.35 g + 1.50 w000d + 0.75 sv |
| 7 | 1.35 g + 1.50 sv + 0.90 w000d |
| 8 | 1.35 g + 1.50 w000d + 0.75 s1 |
| 9 | 1.35 g + 1.50 s1 + 0.90 w000d |
| 10 | 1.35 g + 1.50 w000d + 0.75 s2 |
| 11 | 1.35 g + 1.50 s2 + 0.90 w000d |
| 12 | 1.35 g + 1.50 w000s |
| 13 | 1.35 g + 1.50 w000s + 0.75 sv |
| 14 | 1.35 g + 1.50 sv + 0.90 w000s |
| 15 | 1.35 g + 1.50 w000s + 0.75 s1 |
| 16 | 1.35 g + 1.50 s1 + 0.90 w000s |
| 17 | 1.35 g + 1.50 w000s + 0.75 s2 |
| 18 | 1.35 g + 1.50 s2 + 0.90 w000s |
| 19 | 1.35 g + 1.50 w090d |
| 20 | 1.35 g + 1.50 w090d + 0.75 sv |
| 21 | 1.35 g + 1.50 sv + 0.90 w090d |
| 22 | 1.35 g + 1.50 w090d |
| 23 | 1.35 g + 1.50 w090d + 0.75 sv |
| 24 | 1.35 g + 1.50 sv + 0.90 w090d |
| 25 | 1.35 g + 1.50 w090d + 0.75 s1 |
| 26 | 1.35 g + 1.50 s1 + 0.90 w090d |
| 27 | 1.35 g + 1.50 w090d + 0.75 s2 |
| 28 | 1.35 g + 1.50 s2 + 0.90 w090d |
| 29 | 1.35 g + 1.50 w090s |
| 30 | 1.35 g + 1.50 w090s + 0.75 sv |
| 31 | 1.35 g + 1.50 sv + 0.90 w090s |
| 32 | 1.35 g + 1.50 w090s + 0.75 s1 |
| 33 | 1.35 g + 1.50 s1 + 0.90 w090s |
| 34 | 1.35 g + 1.50 w090s + 0.75 s2 |
| 35 | 1.35 g + 1.50 s2 + 0.90 w090s |
| 36 | 1.35 g + 1.50 w180s |
| 37 | 1.35 g + 1.50 w180s + 0.75 sv |
| 38 | 1.35 g + 1.50 sv + 0.90 w180s |
| 39 | 1.35 g + 1.50 w180s + 0.75 s1 |
| 40 | 1.35 g + 1.50 s1 + 0.90 w180s |
| 41 | 1.35 g + 1.50 w180s + 0.75 s2 |
| 42 | 1.35 g + 1.50 s2 + 0.90 w180s |
| 43 | 1.35 g + 1.50 w180d |
| 44 | 1.35 g + 1.50 w180d + 0.75 sv |
| 45 | 1.35 g + 1.50 sv + 0.90 w180d |
| 46 | 1.35 g + 1.50 w180d + 0.75 s1 |
| 47 | 1.35 g + 1.50 s1 + 0.90 w180d |
| 48 | 1.35 g + 1.50 w180d + 0.75 s2 |
| 49 | 1.35 g + 1.50 s2 + 0.90 w180d |
Oznaczenie symboli w tabelce:
- g – obciążenia stałe
- s1 – obciążenie śniegiem wariant 1 (nierównomierne obciążenie śniegiem dachu, maksymalne obciążenie lewej połaci dachu)
- s2 – obciążenie śniegiem wariant 2 (nierównomierne obciążenie śniegiem dachu, maksymalne obciążenie prawej połaci dachu)
- sv – obciążenie śniegiem całkowite (równomierne obciążenie śniegiem dachu)
- w000d – wiatr 0⁰ max – (wiatr z lewej strony maksymalna wartość obciążenia)
- w000s – wiatr 0 min – (wiatr z lewej strony minimalna wartość obciążenia)
- w090d – wiatr 90⁰ max – (wiatr prostopadle maksymalna wartość obciążenia)
- w090s – wiatr 90⁰ min – (wiatr prostopadle minimalna wartość obciążenia)
- w180d – watr 180⁰ max – (wiatr z prawej strony maksymalna wartość obciążenia)
- w180s – wiatr 180⁰ min – (wiatr z prawej strony minimalna wartość obciążenia)
Stan graniczny użytkowalności (SGU) – kombinacje obciążeń
Kombinacje obciążenia dla stanu granicznego użytkowalności wyznaczają odkształcenia konstrukcji, zależne od wartości charakterystycznych efektów oddziaływań na konstrukcję. Kombinacje dla SGU w programie DC-Statik stworzone są według poniższego wzoru normowego :
oznaczenia:
γQi– współczynnik bezpieczeństwa
Gkj – obciążenia stałe
Qk1 , Qkj – obciążenia zmienne
Ψ0i – współczynnik jednoczesności obciążeń
Przykładowa kombinacja obciążeń dla schematu obliczeniowego – KROKIEW
| Nr kombinacji | Formuła kombinacji |
|---|---|
| 1 | g + sv |
| 2 | g + s1 |
| 3 | g + s2 |
| 4 | g + w000d |
| 5 | g + w000d + 0.50 sv |
| 6 | g + sv + 0.60 w000d |
| 7 | g + w000d + 0.50 s1 |
| 8 | g + s1 + 0.60 w000d |
| 9 | g + w000d + 0.50 s2 |
| 10 | g + s2 + 0.60 w000d |
| 11 | g + w000s |
| 12 | g + w000s + 0.50 sv |
| 13 | g + sv + 0.60 w000s |
| 14 | g + w000s + 0.50 s1 |
| 15 | g + s1 + 0.60 w000s |
| 16 | g + w000s + 0.50 s2 |
| 17 | g + s2 + 0.60 w000s |
| 18 | g + w090d |
| 19 | g + w090d + 0.50 sv |
| 20 | g + sv + 0.60 w090d |
| 21 | g + w090d + 0.50 s1 |
| 22 | g + s1 + 0.60 w090d |
| 23 | g + w090d + 0.50 s2 |
| 24 | g + s2 + 0.60 w090d |
| 25 | g + w090s |
| 26 | g + w090s + 0.50 sv |
| 27 | g + sv + 0.60 w090s |
| 28 | g + w090s + 0.50 s1 |
| 29 | g + s1 + 0.60 w090s |
| 30 | g + w090s + 0.50 s2 |
| 31 | g + s2 + 0.60 w090s |
| 32 | g + w180s |
| 33 | g + w180s + 0.50 sv |
| 34 | g + sv + 0.60 w180s |
| 35 | g + w180s + 0.50 s1 |
| 36 | g + s1 + 0.60 w180s |
| 37 | g + w180s + 0.50 s2 |
| 38 | g + s2 + 0.60 w180s |
| 39 | g + w180d |
| 40 | g + w180d + 0.50 sv |
| 41 | g + sv + 0.60 w180d |
| 42 | g + w180d + 0.50 s1 |
| 43 | g + s1 + 0.60 w180d |
| 44 | g + w180d + 0.50 s2 |
| 45 | g + s2 + 0.60 w180d |